本記事では、代表的なアルゴリズムとしてよく登場する「探索」「併合(マージ)」「整列(ソート)」に注目し、線形探索法や2分探索法といった探索のアルゴリズム、選択ソート・バブルソート・クイックソートといった整列のアルゴリズムを、それぞれのイメージや特徴とともに分かりやすく整理します。
1. 探したいデータを見つけるアルゴリズム

この章では、データの中から目的の値を探し出す「探索のアルゴリズム」について、全体的な考え方を押さえたうえで、線形探索法と2分探索法という代表的な手法を順に確認していきます。
探索のアルゴリズム
探索のアルゴリズムとは、多数のデータの中から「探したい値」がどこにあるか、あるいは存在するかどうかを調べるための手順のことです。身近な例でいえば、名簿から特定の名前を探したり、棚の中から目的の本を探したりする作業が探索にあたります。コンピュータの世界では、配列やリストなどに格納されたデータを対象に、効率よく目的の値を見つける方法が求められます。
探索では、「データが並んでいる順番」や「事前に整列されているかどうか」によって、取るべき方法が変わってきます。あらかじめソートされていないデータなら、端から順に調べる方法が素直ですし、昇順に整列されているなら、真ん中を見ながら絞り込む方法が有効です。こうした違いを意識しておくと、状況に応じてどの探索アルゴリズムが向いているかを判断しやすくなります。
線形探索法
線形探索法は、データを先頭から末尾まで順番に調べていく、とても素直な探索方法です。名簿を上から順に見ていき、探している名前を見つけたらそこで止め、なければ最後まで見て「見つからなかった」と判断するイメージです。データが特別な順番で並んでいなくても使えるのが大きな利点です。
ただし、探すデータが増えるほど、調べる件数もほぼそれに比例して増えてしまいます。目的の値が一番最後にあったり、そもそも存在しなかったりする場合は、すべてのデータを確認する必要があります。そのため、データ件数が少ないときや、あまり頻繁に探索を行わない場面ではシンプルで扱いやすい一方、大量のデータを何度も検索する用途にはあまり向きません。
2分探索法
2分探索法は、あらかじめ昇順や降順に整列されたデータに対して使える、効率の良い探索方法です。ざっくり言うと、「真ん中を見て、探したい値がそれより小さいか大きいかで、見る範囲を半分に絞っていく」という手順を繰り返します。辞書で単語を探すときに、いきなり真ん中あたりを開き、「まだ前だな」「もっと後だな」とページを絞り込んでいく感覚に近いです。
2分探索法の強みは、データの件数が増えても、調べる回数が比較的ゆるやかに増えることです。範囲を半分、半分と絞っていくので、10件・100件・1,000件…と増えても、必要なステップ数の増え方は線形探索よりずっと穏やかです。ただし、前提として「データが整列済みであること」が必要なので、整列にかかるコストとのバランスを考えることが重要になります。
2. データを並べ替えるアルゴリズム

この章では、データを一定の順番に並べ替える「整列(ソート)のアルゴリズム」について、全体像を確認したうえで、選択ソート・バブルソート・クイックソートという代表的な手法の特徴を比べていきます。
整列のアルゴリズム
整列のアルゴリズムは、データを「小さい順」「大きい順」「五十音順」など、決められたルールに従って並べ替えるための手順です。名簿をあいうえお順に並べたり、テストの点数順に並べたりする作業をイメージすると分かりやすいでしょう。コンピュータでは、検索を効率よく行うための前処理としてソートが行われることも多くあります。
整列のアルゴリズムは、一見同じように並べ替えているようでいて、その手順や効率に大きな違いがあります。データ数が少なければどの方法でもあまり差が出ませんが、数が増えるほど「何回くらい比較や入れ替えを行うことになるのか」が性能に大きく影響します。ここでは、代表的な三つのアルゴリズムのざっくりとしたイメージを押さえることが目的です。
選択ソート
選択ソートは、「まだ並べていない中から一番小さい(または大きい)ものを探して、左から順に確定していく」という考え方の整列方法です。具体的には、まず全体から最小値を探して先頭の要素と入れ替え、次に残りの部分から最小値を探して2番目の場所に入れ…という操作を、最後の要素になるまで繰り返します。
この方法は、「何をしているのか」が非常にイメージしやすいのが利点です。一方で、各ステップで最小値を探すために残りの要素を一通り調べる必要があり、データ数が多くなると比較の回数が急激に増えてしまいます。学習用の例としては扱いやすいものの、大量データ向けの実用的なソートとしては、もっと効率の良い手法が選ばれることが多いです。
バブルソート
バブルソートは、隣り合う要素を見比べて、順番が逆なら入れ替える操作を、何度も繰り返す整列方法です。水槽の中で小さな泡が少しずつ上に上がっていくイメージから「バブル」という名前がついています。配列の先頭から末尾まで順番に見ていき、隣どうしを入れ替えていくことで、大きな値がだんだん端に押し出されていきます。
バブルソートも、動きをアニメーションなどで表すと直感的に理解しやすい方法です。しかし、並びが悪いと、何度も何度も配列の端から端まで比較と入れ替えを繰り返すことになり、効率はあまり良くありません。そのため、こちらも学習用途としては有名ですが、実務レベルではより高速なアルゴリズムが使われるのが一般的です。
クイックソート
クイックソートは、実用的な整列アルゴリズムとしてよく使われる方法の一つです。ざっくり言うと、「基準となる値(ピボット)を一つ選び、それより小さいグループと大きいグループにデータを分け、同じ操作をグループごとに再帰的に繰り返す」という手順で並べ替えていきます。大きな山を「小さい山」と「大きい山」に分け、それぞれをまた小さな山に分けていくイメージです。
クイックソートは、平均的には非常に効率よく整列を行えるのが特徴です。データを分割しながら処理するため、比較や入れ替えの回数を抑えやすく、大量のデータでも高速に動作します。ただし、データの並びによっては効率が落ちるケースもあり、実際の実装では、基準値の選び方を工夫するなどの対策が行われます。ITパスポート試験のレベルでは、「分割を繰り返して効率よく並べ替える方法」というイメージを持っておくと十分です。
3. 併合(マージ)とアルゴリズムの活用
この章では、複数のデータ列を一つにまとめる「併合(マージ)」の考え方を確認しながら、探索や整列と組み合わせてアルゴリズムをどのように活用していくかをイメージしていきます。
併合(マージ)の考え方
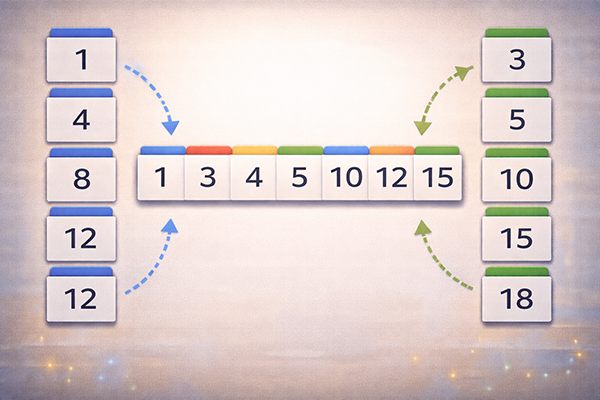
併合(マージ)とは、複数のデータ列を一つにまとめる処理のことです。特に、すでに整列されている二つの列を、順番を保ったまま一つの整列済みの列にまとめる操作がよく扱われます。例えば、「A店の売上データ」「B店の売上データ」がそれぞれ日付順に並んでいるときに、両方を合わせて一つの時系列データにしたい、といった場面です。
整列済みの二つの列をマージする場合、先頭どうしを比べて小さい方を結果の列に移し、その列の次の要素ともう一方の先頭をまた比べる、という操作を繰り返すのが基本です。この方法を使うと、両方の列を全部確認しながらも、余計な並べ替えをすることなく、効率よく併合が行えます。ソートアルゴリズムの中には、このマージの考え方を組み込んだ「マージソート」という手法も存在します。
探索・整列アルゴリズムと効率のイメージ
探索・整列・併合のアルゴリズムは、それぞれ単体で使われるだけでなく、組み合わせることで実用的な処理を構成します。例えば、大量のデータをまずクイックソートで整列し、その後に2分探索法で素早く検索する、といった使い方です。また、複数の拠点から集まってくるデータを、各拠点で整列しておき、最後にマージでまとめるという設計も考えられます。
アルゴリズムを選ぶときには、「データがどのくらいの量なのか」「すでに整列されているのか」「どの処理を何回くらい行うのか」といった条件によって、向き・不向きが変わります。ITパスポート試験の学習では、細かい計算量の式を覚えるよりも、「線形探索や単純なソートは分かりやすいが遅くなりやすい」「2分探索やクイックソートは工夫によって効率を上げている」といった大まかな特徴をイメージしておくことが大切です。
まとめ
本記事では、代表的なアルゴリズムとして、データを探す探索アルゴリズム、データを順番に並べる整列アルゴリズム、複数のデータ列をまとめる併合(マージ)の考え方を取り上げました。それぞれの役割を区別しながら、どんな場面で使われるのかをイメージできることが第一歩になります。
探索では、どんな並び方のデータにも使える線形探索法と、整列済みデータに対して真ん中から絞り込んでいく2分探索法を紹介しました。整列では、分かりやすさを重視した選択ソート・バブルソートと、実用性の高いクイックソートを比べることで、「同じ並べ替えでも効率に差が出る」ことを確認しました。さらに、整列された複数の列を効率よく一つにまとめる併合(マージ)の考え方も押さえました。
アルゴリズムの学習では、専門的な数式よりも、「実際の作業に置き換えるとどんな手順か」「データが増えたときにどれくらい大変になりそうか」といった直感を持つことが重要です。代表的な探索・整列アルゴリズムのイメージをつかんでおけば、試験問題でフローチャートや擬似言語が出てきたときにも、「この部分は線形探索っぽい」「ここはクイックソートのように分割している」といった形で読み解きやすくなります。基礎的なアルゴリズムの特徴をしっかり押さえ、実際の処理の流れを頭の中で追いかける練習を重ねていくことが、理解を定着させる近道です。


コメント