本記事では、グラフ理論の基本的な考え方とグラフの読み取り方について解説します。頂点や辺といった用語の意味をしっかり押さえたうえで、有向グラフ・無向グラフの違いを理解し、最後にグラフをどのような手順で読み解けばよいかを整理することで、ネットワークや経路探索などの問題を論理的に把握できるようになることを目指します。
1. グラフ理論で何が表現できるのか

この章では、グラフ理論がどのような場面で使われるのか、そしてグラフを構成する基本部品としての「頂点」と「辺」について説明します。抽象的に聞こえるグラフ理論も、実は身の回りの仕組みをそのまま図にしただけだと分かれば、ぐっと理解しやすくなります。
例えば、駅同士を結ぶ路線図、SNSにおける友達関係、業務フローにおける作業のつながりなどは、いずれもグラフとして表すことができます。対象となるモノや人を点として置き、それらの間の関係やつながりを線として表現することで、複雑な構造を整理して眺めることができるのです。
頂点(ノード)
頂点とは、グラフを構成する「点」の部分であり、ノードと呼ばれることもあります。駅を表す点、倉庫を表す点、システム同士の接続関係におけるサーバを表す点など、対象となる実体を抽象的に表現したものが頂点です。図の中では丸や四角などの記号で描かれ、名前や番号が付けられることが多くなります。
頂点を意識してグラフを見ると、「どんなもの同士の関係を扱っているのか」がはっきり分かるようになります。同じグラフでも、頂点を人とみなすのか、会社とみなすのかで、読み取れる意味がまったく変わってきます。問題文では、頂点が何を表しているのかが必ず説明されるので、最初にそこを丁寧に確認することが大切です。
辺(エッジ)
辺とは、頂点同士を結ぶ「線」の部分であり、エッジと呼ばれます。二つの頂点の間に何らかの関係があることを表現するのが辺の役割です。たとえば、二つの駅の間に電車が走っていること、二つの人が友達であること、一方の作業が終わると次の作業に進むことができるといった関係を、一本の辺で示すことができます。
辺には、単に「つながっている」ことだけを示す場合もあれば、「距離」「時間」「コスト」といった重みが付く場合もあります。ITパスポート試験のレベルでは、まずは「どの頂点とどの頂点が結ばれているのか」を正しく読み取り、そのつながり方から全体の構造を把握できれば十分です。慣れてくると、どの辺が重要なのか、どこがボトルネックになりそうかといった視点も持てるようになります。
2. 有向グラフと無向グラフの違いを理解する
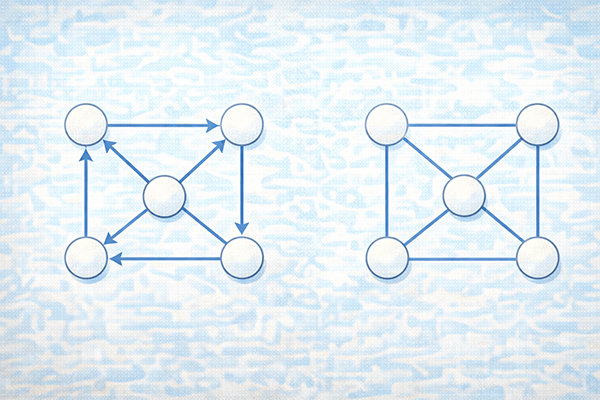
この章では、グラフの中でも特によく登場する「有向グラフ」と「無向グラフ」について説明します。どちらも頂点と辺で構成されていますが、辺に「向き」があるかどうかによって、表現できる関係の意味合いが大きく変わります。
試験問題では、図を一目見てそれが有向グラフなのか無向グラフなのかを判断し、その前提に沿って関係性を読み取ることが求められます。矢印の有無だけを機械的に見るのではなく、「この関係は向きがあるのか、ないのか」という意味を意識して図を眺める癖をつけておきましょう。
有向グラフ
有向グラフとは、辺に向きがあるグラフです。辺は単なる線ではなく矢印で描かれ、「どちらからどちらへ」という一方向の関係を表します。例えば、「A さんが B さんにメッセージを送った」「工程 A のあとに工程 B を行う」「Web ブラウザから Web サーバにリクエストを送る」といった、始点と終点がはっきりしている関係は有向グラフで表すのに適しています。
有向グラフを見るときは、どの頂点から矢印が出ていて、どの頂点に矢印が入っているのかを丁寧に追いかけることが重要です。矢印の流れをたどることで、「処理の順番」「情報の流れ」「依存関係」などが把握しやすくなります。逆に、矢印の向きを無視して読んでしまうと、順番を取り違えたり、実際には到達できない経路を誤って選んでしまうことがあるので注意が必要です。
無向グラフ
無向グラフとは、辺に向きがないグラフです。辺は両端を結ぶ線として描かれ、どちらが始点でどちらが終点かは区別されません。「A 駅と B 駅の間に線路がある」「A さんと B さんは友達関係である」「二つのコンピュータ同士が相互に接続されている」といった、対等なつながりを表すのに適したグラフです。
無向グラフでは、辺が存在するだけで「相互に行き来できる」「お互いに関係がある」ということを意味します。そのため、図を読むときは、単に線が引かれているかどうかと、どの頂点がどのくらい多くの頂点とつながっているかに注目するとよいでしょう。つながりが多い頂点は、ネットワークのハブであったり、重要な拠点であることが多く、全体の構造を理解する手がかりになります。
3. グラフの読み取り方と活用イメージ

この章では、これまで学んだ概念を踏まえて、グラフをどのような手順で読み解いていけばよいのか、その考え方をいくつかの視点に分けて紹介します。最初は難しく見える図でも、決まった順番で確認していけば、構造のポイントを落ち着いてつかむことができます。
グラフを読むときの基本手順
グラフを読むときは、まず問題文から「頂点が何を表し、辺が何を表しているのか」を丁寧に確認します。頂点が人なのか、システムなのか、作業工程なのかによって、同じ形の図でも意味が大きく変わるからです。次に、そのグラフが有向グラフなのか無向グラフなのかを確認し、矢印の有無に応じて「流れ」を追うべきか「つながり」を見るべきかを意識します。
ここまで確認できたら、図全体を眺めて「頂点はいくつあるか」「どの頂点がよく線で結ばれているか」といった、構造の大まかな特徴をつかみます。最初から細かい経路を追いかけるのではなく、全体像をざっくり把握してから細部を確認することで、読み間違いを減らすことができます。
経路とつながりをたどるコツ
経路を問う問題では、「ある頂点から別の頂点へ到達するには、どのようなルートがあるか」を考えることになります。有向グラフの場合は矢印の向きを必ず守りながら、矢印の流れに沿って進めるかどうかを確かめます。無向グラフの場合は矢印がないため、線が引かれていればどちら向きにも行けると考えて構いません。
経路が複雑なときは、紙の上で実際にたどりながら、通った頂点や辺に印を付けて整理すると分かりやすくなります。また、「最短経路」を聞かれているのか、「通れるかどうか」だけを聞かれているのかを意識することも重要です。最短経路であれば、通過する辺の数や重みを比較しながら、無駄なく目的地に到達できるルートを探します。
ネットワーク構造を理解する視点
グラフ理論の問題では、ネットワーク構造そのものの性質を問うケースもあります。例えば、「ある頂点が故障すると、どの頂点同士の連絡が取れなくなるか」「特定の頂点が一つだけ他の頂点とつながっている」など、つながり方の特徴から役割を読み取る問題です。このときは、一つ一つの頂点の位置関係や、つながりの多さに注目すると理解しやすくなります。
つながりが特に多い頂点は、ネットワークのハブや重要拠点である可能性が高く、その頂点にトラブルが起きると大きな影響が出ます。一方で、たった一つの頂点を通らないと別の領域に行けないような構造になっている場合、その頂点は「ボトルネック」や「橋渡し役」として機能していると考えられます。こうした視点を持ってグラフを見ることで、単なる線の集合ではなく、ネットワーク全体の性質を立体的に理解できるようになります。
まとめ
本記事では、グラフ理論の基本となる考え方と、頂点・辺・有向グラフ・無向グラフといった主要な用語について解説し、最後にグラフの具体的な読み取り方を確認しました。グラフは、複雑なつながりをシンプルな図で表現するための道具であり、駅同士の関係や人間関係、システム間の接続など、日常のさまざまな構造を扱うことができます。
頂点(ノード)は「何を対象としているのか」、辺(エッジ)は「どのような関係があるのか」を表し、有向グラフか無向グラフかによって、その関係が一方向なのか相互なのかが決まります。図を見るときには、まずこれらの意味を押さえたうえで、どの頂点がどことつながっているのか、矢印はどちら向きなのかに注目することが大切です。
グラフの読み取り方に慣れてくると、ネットワークの構造や処理の流れを、直感的かつ論理的に把握できるようになります。IT分野だけでなく、ビジネスの業務プロセスや組織の関係を整理する場面でも役立つ考え方なので、図を見かけたら「これはどんな頂点と辺でできたグラフなのだろう」と意識して眺めてみてください。そうした日常的な意識づけが、グラフ理論の理解を自然と深めてくれます。


コメント