本記事では、自然言語の文章を論理的に整理して表現する考え方と、その際に重要となる「述語論理」「演繹推論」「帰納推論」について解説します。日常のあいまいな言い回しを、コンピュータにも伝わる形に整理する視点を押さえることで、試験だけでなく実務での説明力や問題解決力の向上にもつながります。
1. 自然言語の文章を論理的に表現するイメージ

この章では、私たちがふだん使っている日本語の文章を、論理的な構造に分解して表現するとはどういうことかを全体像として確認します。論理的な記述の基本的な流れや、なぜ記号化・形式化が役立つのかをイメージできるようにすることがねらいです。
自然言語と論理的表現の違い
自然言語の文章は、人間にとっては分かりやすくても、あいまいさや解釈の幅を含んでいることが多いです。たとえば「条件を満たす人には手当を支給する」というルールを考えたとき、人によって「条件」の理解が微妙に違ってしまうと、公平な運用ができません。表現にゆれがあると、「ある人にとっては支給対象」「別の人にとっては対象外」と判断が分かれてしまうこともあります。
論理的な記述では、このようなあいまいさをできるだけ取り除くために、「対象は何か」「どんな条件を満たすときに成り立つのか」「その結果どうなるのか」といった要素を切り分けます。そして、それぞれを一定のルールに従って記号や記述形式で表すことで、誰が読んでも同じ意味に解釈できる文章を目指します。自然言語のままではぼんやりしていた構造を、骨組みとしてはっきりさせるイメージです。
記号を用いた表現のメリット
記号を用いて論理的に表現する最大のメリットは、解釈のぶれを小さくできることです。条件や結論を記号で表し、「AならばBである」といった形で書いておくと、途中で言い回しを変えても意味が変わらないように管理できます。人間同士でも誤解が生じにくくなりますし、チェックやレビューもしやすくなります。
さらに、記号による表現は、そのままプログラムや仕様書に落とし込むことにも向いています。コンピュータはあいまいな表現を理解できないため、「どの条件のときに、どの処理を行うのか」を論理的に記述しておくことが不可欠です。こうした背景から、自然言語の文章を論理的に整理して表現するスキルは、情報分野において基礎的でありながら、とても重要な役割を担っています。
2. 述語論理で「誰にでも通用する形」に直す
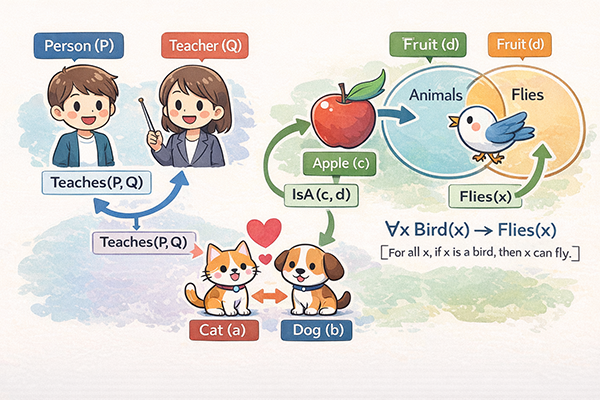
この章では、「Aさんは学生である」などの文を、より構造化された形で表現するための考え方である述語論理について説明します。どのような部品に分けて文を捉えるのか、そしてそれが論理的な記述にどう役立つのかを押さえることが目的です。
述語論理
述語論理では、文章を「対象」と「性質や関係」に分けて表現します。たとえば「太郎は学生である」という文は、「太郎」という対象と、「〜は学生である」という性質に分けて考えます。これを記号で表すと、対象をあらわす部分を変数や定数(Taro など)、性質の部分を述語(Student(x) など)として、「Student(Taro)」のように書き表します。こうすることで、文の構造がはっきりと見えるようになります。
また、「すべての学生はレポートを提出する」といった文は、個別の人を列挙するのではなく、「すべての〜」「ある〜が存在する」といった量を表す記号を使って表現します。これにより、「どの範囲の対象について成り立つ主張なのか」を明確にできます。述語論理は、一見すると難しそうに見えますが、要するに「主語」「述語」「対象の範囲」といった要素をきちんと切り分けて書き表すためのルールだと考えると理解しやすくなります。
3. 規則から結論を導く演繹推論
この章では、与えられた前提やルールから、論理的に必然といえる結論を導き出す「演繹推論」について解説します。規則に従って考えを進める際の典型的なパターンを押さえることで、仕様やマニュアルを読む力も高められます。
演繹推論
演繹推論とは、「一般的なルール」や「前提」が正しいと仮定したうえで、そこから個々の結論を導き出す推論方法です。たとえば「すべての社員はIDカードを携帯する」「山田さんは社員である」という前提があれば、「山田さんはIDカードを携帯する」という結論が論理的に導けます。このとき、前提が正しく、推論の手順にも誤りがなければ、結論も必ず正しいとみなされます。
ITの世界では、仕様書やルールを元に「このケースではどうなるか」を判断する場面で演繹推論が活躍します。セキュリティポリシーや社内規程など、あらかじめ決められた条件を当てはめて判断する考え方そのものが演繹推論です。問題演習でも、「与えられた条件が前提」「選択肢の内容が結論」と考え、前提と結論のつながりに矛盾がないかをチェックする習慣をつけると、正答を選びやすくなります。
4. 事例から一般法則を見つける帰納推論
この章では、複数の具体例から共通点を見出し、「おそらくこうだろう」という一般的なルールを考える帰納推論について説明します。データ分析や改善活動など、実務で頻繁に使われる考え方なので、演繹推論との違いも意識しながら理解しておくことが大切です。
帰納推論
帰納推論は、個々の観察結果や事例から、より一般的な結論を導き出す推論方法です。たとえば、あるサービスで「問い合わせの多くが夜間に集中している」「夜間はオペレーターが少ない」というデータが続けて観測されたとします。このような具体的な事実を積み重ねて、「夜間帯は人員不足になりやすい」「夜間にサポート体制を強化すべきだ」といった一般的な判断につなげるのが帰納推論の典型的な使い方です。
ただし、帰納推論の結論は「必ず正しい」とは限らず、「そのデータが示す範囲では妥当そうだ」というレベルのものにとどまります。たまたま偏ったデータを見ていたり、サンプル数が少なかったりすると、誤った一般化をしてしまう危険もあります。そのため、帰納推論を行うときには、データの量や質、例外の有無などにも注意する必要があります。情報分野では、アクセスログやアンケート結果などから傾向を読み取るときに、無意識のうちに帰納推論を行っていると考えるとイメージしやすいでしょう。
まとめ
論理的な記述とは、日常の自然言語の文章を、対象・条件・結論といった要素に分け、記号や一定のルールを使って整理して表現することです。その土台として、文章を構造化して捉える述語論理があり、そこから結論を導く過程として演繹推論や帰納推論といった考え方があります。どれも、あいまいな言い方をできるだけ避け、誰が読んでも同じ意味に解釈できるようにするための道具だと捉えると理解しやすくなります。
演繹推論は、与えられた前提やルールが正しい限り、結論も必ず正しいと言えるという特徴があります。一方、帰納推論は、観測された事例やデータから「一般的にはこうだろう」と推測する方法であり、結論はあくまで「高い確からしさ」を持つにとどまります。この違いを押さえておくと、問題を解くときにも「ここはルールの当てはめ」「ここはデータからの推測」と、頭の中で整理しながら考えられるようになります。
論理的な記述や推論の考え方を身につけておくと、試験対策だけでなく、仕様の読み取り、トラブルの原因分析、業務改善の提案など、さまざまな場面で役立ちます。日常の会話や文章の中でも、「これはどんな前提と結論の関係になっているか」「これは事例から一般化しているのか」と意識してみることで、論理的に考える力を少しずつ鍛えていくことができます。

の技術-300x158.png)
コメント