【ITパスポート試験】No.087｜集合

本記事では、「集合」と呼ばれる考え方を出発点に、命題・ベン図・真理値表といった論理の道具をまとめて学びます。どれも数学の話に聞こえますが、条件分岐を考えるプログラムや、顧客分析・アクセス解析など、情報処理やビジネスの現場で幅広く使われる考え方です。ITパスポート試験でも頻出の範囲なので、用語の意味と、実際にどう役立つのかをセットで押さえていきましょう。

1.　集合と命題の基本をつかむ

この章では、「どんなものが集まっているか」を丁寧に分けて考える集合の考え方と、「〜である」「〜でない」とはっきり言い切る命題について整理します。どちらも、あいまいな状態を整理して、条件をはっきりさせるための道具だとイメージできると理解しやすくなります。

集合とは

集合とは、「ある共通の性質をもつものを1つのグループとしてまとめたもの」です。例えば、「Aクラスの生徒」「20代の顧客」「首都圏在住のユーザー」などは、いずれも集合として捉えられます。共通点を決め、その条件を満たすものだけを集めた箱のようなイメージを持つとよいでしょう。

集合では、しばしば英大文字（A, B, C など）で集合そのものを表し、その中身である要素を小文字（a, b, c など）で表すことがあります。「a は集合Aに属する」という意味で「a∈A」と書くこともありますが、ITパスポート試験では、厳密な記号よりも言葉で理解できていれば十分です。

現実の業務では、顧客リストを「購入経験のある人の集合」「メルマガ登録者の集合」「30代の集合」のように分けて分析します。どの集合に属しているかを整理することで、「どんな人がよく買っているのか」「どの条件を満たす人にキャンペーンを送るか」といった判断がしやすくなります。

命題とは

命題とは、「真（正しい）か偽（誤り）かがはっきり決まる文」のことです。例えば、「Aさんは20代である」「今日の売上は100万円を超えた」は、真か偽かを判定できますので命題です。一方で、「この商品はかっこいい」「ご飯はおいしい」といった好みや感想は、人によって評価が変わるので命題とはみなしません。

命題を扱う理由は、条件判断を論理的に整理するためです。例えば「在庫がある かつ 顧客が会員登録済みであるなら、割引を適用する」といったビジネスルールは、それぞれの条件を命題として捉えると明確になります。プログラムの if 文や、業務マニュアルの「〜の場合は〜する」といった分岐は、命題を組み合わせたものだと考えられます。

命題は後で登場する真理値表と組み合わせることで、「条件を組み合わせると結果はどう変わるか」を一覧で確認できるようになります。集合と命題は、どちらも「対象を整理して条件を明確にする」ための基礎となる考え方だと押さえておきましょう。

2.　ベン図で集合の関係を視覚化する

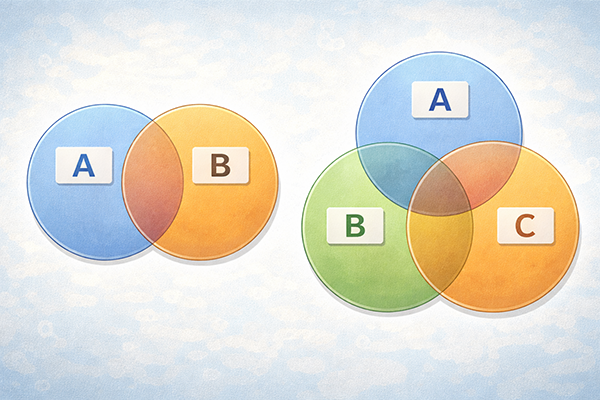
この章では、集合同士の関係を図でわかりやすく表すベン図を扱います。頭の中だけで「Aの集合とBの集合が重なるところ」と考えると複雑に感じますが、ベン図を使うと、重なり方や違いが一目で確認できます。試験でも定番の図なので、描き方と読み取り方をセットで理解しておくことが大切です。

ベン図とは

ベン図とは、集合を円で表し、その重なり方で関係を示す図のことです。例えば、「A：英語が得意な人の集合」「B：数学が得意な人の集合」とした場合、AとBの両方に属する人は、2つの円が重なっている部分に位置付けられます。Aだけに属する人はAの円のうち、Bと重ならない部分に入ります。

ベン図では、主に次のような関係を読み取ります。

例えば、顧客を「最近1か月以内に購入した集合」と「メルマガ登録者の集合」に分けた場合、両方の集合に含まれる人は「購入もしていてメルマガも読んでいる、関心の高い顧客」と考えられます。一方、メルマガだけ登録して購入していない人は「見込み顧客」、購入したがメルマガは登録していない人は「ファンだが情報発信が届いていない層」といったように、重なり方からビジネスの示唆を得ることができます。

このように、ベン図を使うと、複数の集合の関係を視覚的に把握できるため、条件の抜け漏れや重複をチェックする場面にも役立ちます。

3.　真理値表で条件の組み合わせを整理する

この章では、命題を組み合わせたときに結果がどう変化するかを一覧にまとめる真理値表を学びます。条件が1つだけなら直感的に判断できますが、2つ以上の条件を「かつ」「または」「でない」と組み合わせると、頭の中だけでは混乱しやすくなります。真理値表を使うと、すべてのパターンを漏れなく確認できるため、論理的な条件設定に大きな力を発揮します。

真理値表とは

真理値表とは、命題の「真（T：True）」と「偽（F：False）」の組み合わせに対して、論理演算の結果がどうなるかを表形式で示したものです。

例えば、命題Aを「在庫がある」、命題Bを「顧客が会員である」とすると、「A かつ B」（在庫があり、かつ、顧客が会員である）という条件は、AもBも真のときだけ真になります。この関係を整理したものが真理値表です。

代表的な論理演算には次のようなものがあります。

これらの組み合わせを真理値表として並べておくことで、「この条件式はどんなときに真になるのか」を明確に確認できます。例えば、割引キャンペーンの適用条件を見直すときに、「この条件の書き方で本当に狙った顧客だけが対象になっているか」を検証するのに役立ちます。

まとめ

本記事では、集合・命題・ベン図・真理値表という4つのキーワードを通して、「条件を整理して論理的に考える」ための基本的な道具を紹介しました。集合は、共通の性質を持つものを1つのグループとしてまとめる考え方であり、命題はそのグループに属するかどうかを「真」か「偽」かで判断する土台となります。

ベン図は、複数の集合の関係を直感的に把握するための図で、共通部分や違いを目で見て確認できる点が大きな特徴です。真理値表は、命題を組み合わせたときに結果がどう変わるかを、すべてのパターンについて一覧で示す表であり、条件設定の抜け漏れを防ぐのに有効です。

これらの考え方は、数学の問題だけでなく、顧客分析やキャンペーン条件の設計、プログラムの分岐処理など、ビジネスやITのさまざまな場面に共通して役立ちます。言葉や図の意味を理解し、「なぜその道具を使うのか」という目的意識を持って学ぶことで、ITパスポート試験だけでなく、日々の業務の中でも論理的に考える力を高めることができます。